(Offered in Spring 2012)
Class time: 2:35-3:50 Tuesdays and Thursdays
Class location: Olin Hall 134
- Download PDF file of Course Syllabus
- Download PDF file of course flyer here
- See sample final projects offered in Spring 2011.
This is a graduate level course in robotics and mechanism synthesis. The course focuses on covering several topics in kinematics of serial and parallel robots, special methods in kinematics including dual number representations and quaternion methods, introduction to screw-based kinematics and its applications to mechanism analysis and synthesis, line geometry methods and applications in kinematics, open research problems in robotics, mathematical methods for the solution of polynomial systems related to design/analysis problems of mechanisms (e.g. direct kinematics of parallel robots) including homotopy continuation methods and resultant-based methods.
The course is highly recommended for graduate students with some background in robotics and mechanism theory who are interested in expanding their background for research in these areas. It is intended to provide a wider perspective on the mathematical methods and on performance evaluation/optimization of different mechanisms/robots including parallel robots, serial robots, multi-fingered hands, robots with actuation redundancy and with kinematics redundancy (e.g. snakes).
The mathematical background necessary for this course includes linear algebra (you should be familiar with matrix computations, eigenvalues/eigenvectors) and ordinary differential equations (recommended).
Course Administration
This course is open for graduate students interested in strengthening their background in kinematics and robotics. The course grading is based on home works, research projects.
Textbooks
The course will mainly focus on the class notes of the instructor. Most of the topics covered are included in the following recommended text books:
- Fundamentals of Robotic Mechanical Systems, by Jorge Angeles, 2nd Edition (3rd edition is expected soon so check if it is available), Springer, 2003.
- Advanced Robotics, by Yoshihiko Nakamura, Addison-Wesley Publishing Company, 1991 (this book is not in print anymore, but I will be providing some of my own notes based on this book. You will be able to find some used copies of it online)
There are several other books that I will recommend at the beginning of the class. The above-mentioned books are the most relevant to my class - but they do not cover all the topics that I will discuss.
Subjects covered
The course will cover the following topics based on time availability:
- Review of rigid body transformations (Homogeneous matrices, The screw and the screw transformation and the exponential representation of a screw transformation, Transformation verses displacement matrices: the zero-reference method, Calculating the finite displacement screw for a specified motion).
- Special methods in kinematics (Quaternion algebra, rotation vectors, and applications of dual quaternions for kinematic analysis and synthesis).
- Introduction to line geometry (Introduction to projective geometry: homogenous representation of points and lines, The Plücker line coordinates, The independent line varieties in plane and space).
- Introduction to screw theory (Reciprocity and the principle of virtual work, The screw, twist, and wrench systems: the cylindroid, regulus, congruence and linear the complex)
- Instantaneous kinematics of open and closed kinematic chains (Derivation of the instantaneous kinematics Jacobian based on kinematic constraints, Geometric interpretation of the instantaneous kinematics Jacobian of serial and parallel manipulators & applications for line-based singularity analysis, Input-output relationship in closed-loop mechanisms using auxiliary coordinates)
- Kinetostatic analysis of serial and parallel robots ( Alternative derivation of the instantaneous kinematics Jacobian using statics, Screw-based formulation of the Jacobian of parallel and serial robots, Stiffness mapping for parallel and serial robots, Dualities between serial and parallel manipulators, Singularity and Performance indices (kinematic conditining indec, manipulability ellipsoid, stiffness ellipsoid, isotropy, condition number, joint range availability))
- Introduction to redundant manipulators (Singular Value Decomposition, Solution of underdetermined and over-constrained linear system of equations, Task-priority optimization methods for obstacle avoidance, singularity avoidance, and dexterity optimization, Actuation redundancy: optimization of actuator effort, applications to wire-actuated parallel robots and multi-fingered grasping).
- Introduction to numerical and symbolic methods for the solution of polynomial systems arising in kinematics (Direct kinematics of parallel robots and synthesis of spatial mechanisms: motivating examples from the literature, Homogenization of polynomial systems, Root counts for polynomial systems: the Bezout number and the BKK bounds, Introduction to Homotopy continuation methods, Introduction to the theory of elimination: the Dialytic elimination method, The Sylvester and Bezout resultants, Transforming the resultant formulation to an associated generalized eigenvalue problem.
Examples
The following images show some of the robots/topics we will be focusing on in this class. The course is intentionally designed to cover wider topics, but will provide you a prossibility to get familiar with some of these topics for later research.

Example 1: a parallel robot is composed of several closed kinematics chains (RSPR3 robot)
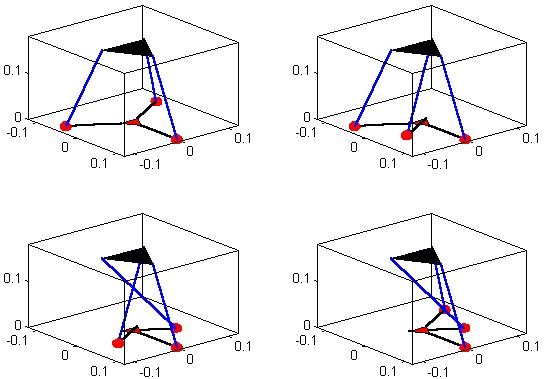
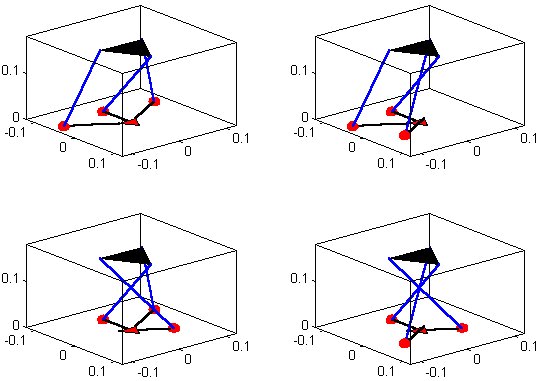
Example 2: eight possible inverse kinematics solutions for a Composite Serial-in-Parallel (CISP) robot RSPR3
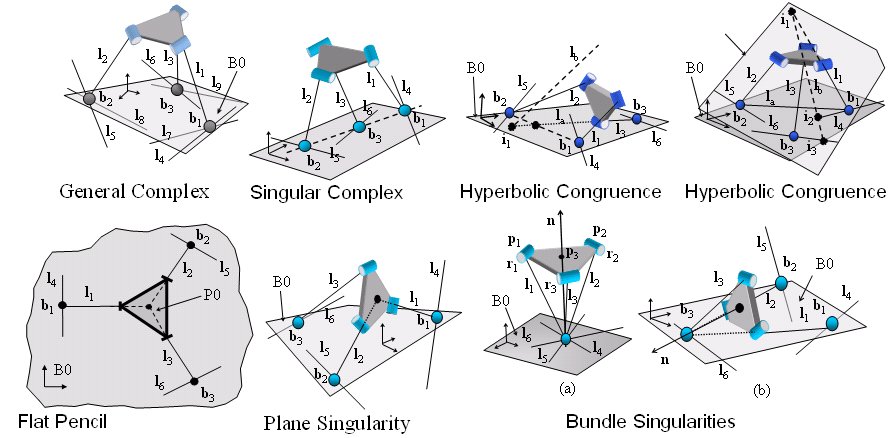
Example 3: The singularities of the RSPR3 robot and other parallel robots can be explained by associating a physical interpretation to the rows of the jacobian and using line geometry.
